탐색적 데이터 분석(Exploratory Data Analysis)

• 방문해주셔서 감사합니다.
• 내용은 지속적으로 업데이트 될 것입니다.
• 궁금한 내용은 댓글로 남겨주세요.

도입(Introduction)

이번 글은 데이터 마이닝의 시작 단계에서 배우는 탐색적 자료 분석, 즉 EDA(Exploratory Data Analysis) 에 관한 글입니다.

EDA의 정의(Definition of EDA)

EDA란 데이터가 어떤 자료로 구성되어있고 분포는 어떠한지를 보는 것입니다.

엑셀이나 데이터베이스에 저장된 데이터를 보면 이 데이터가 어떤 데이터인지 파악하기는 어렵습니다. 그래서 한 눈에 데이터의 구조와 분포를 파악하기 위해 EDA를 하게 됩니다.

EDA의 목적(Purpose of EDA)

항상 어떤 도구를 사용하기 전에 이 도구의 목적이 무엇인지 생각하는 것이 중요합니다.

목적이 무엇인지를 항상 염두해두면, 사용하는 방법론이 진짜 이 목적에 부합하는 것인가를 고민하는데 도움이 되기 때문입니다.

이런 고민을 통해서 목적에 맞는 더 좋은 방법론을 찾을 수 있습니다.

EDA의 목적은 다음과 같습니다.

1. 데이터 수집 단계에서 실수로 입력한 부분이 있는지 확인하기위해서(Detection of mistakes)
2. 데이터에 대한 가정이 맞는지 확인하기위해서(Checking of assumptions)
3. 데이터 유형에 맞는 적절한 모델 선택하기위해서(Preliminary selection of appropriate models)
4. 설명변수들 사이의 관계 파악하기위해서(determining relationships among explanatory variables )
5. 설명변수와 목적변수 사이의 관계 파악하기위해서(assessing the direction and rough size of relationships between explanatory and outcome variables)

갑자기 생각난 사족을 덧붙이자면, 데이터를 분석할때 궁극적으로 모집단(population)의 분포(density)와 모수(parameter)가 어떠한지 아는 것이 제일 좋습니다. 그런데 우리는 모집단의 분포와 모수를 모르기 때문에, 수집된 표본(sample) 데이터를 통해 이를 파악해야합니다. 즉, 데이터를 분석하면서 잊지말아야하는 것은 우리는 표본 데이터를 통해 모집단의 분포와 모수를 추정하고 있다는 것입니다. 그래서 모집단의 분포가 아닌 것 같은 데이터를 찾아내는 것으로 이상치 탐색, outlier detection이 있습니다.

EDA의 종류(Type of EDA)

무엇인가를 정리할때 분류를 통해 정리하는 것은 기억에도 오래 남고 원하는 방법을 찾을때에도 효과적입니다. 따라서 EDA를 분류해보겠습니다.

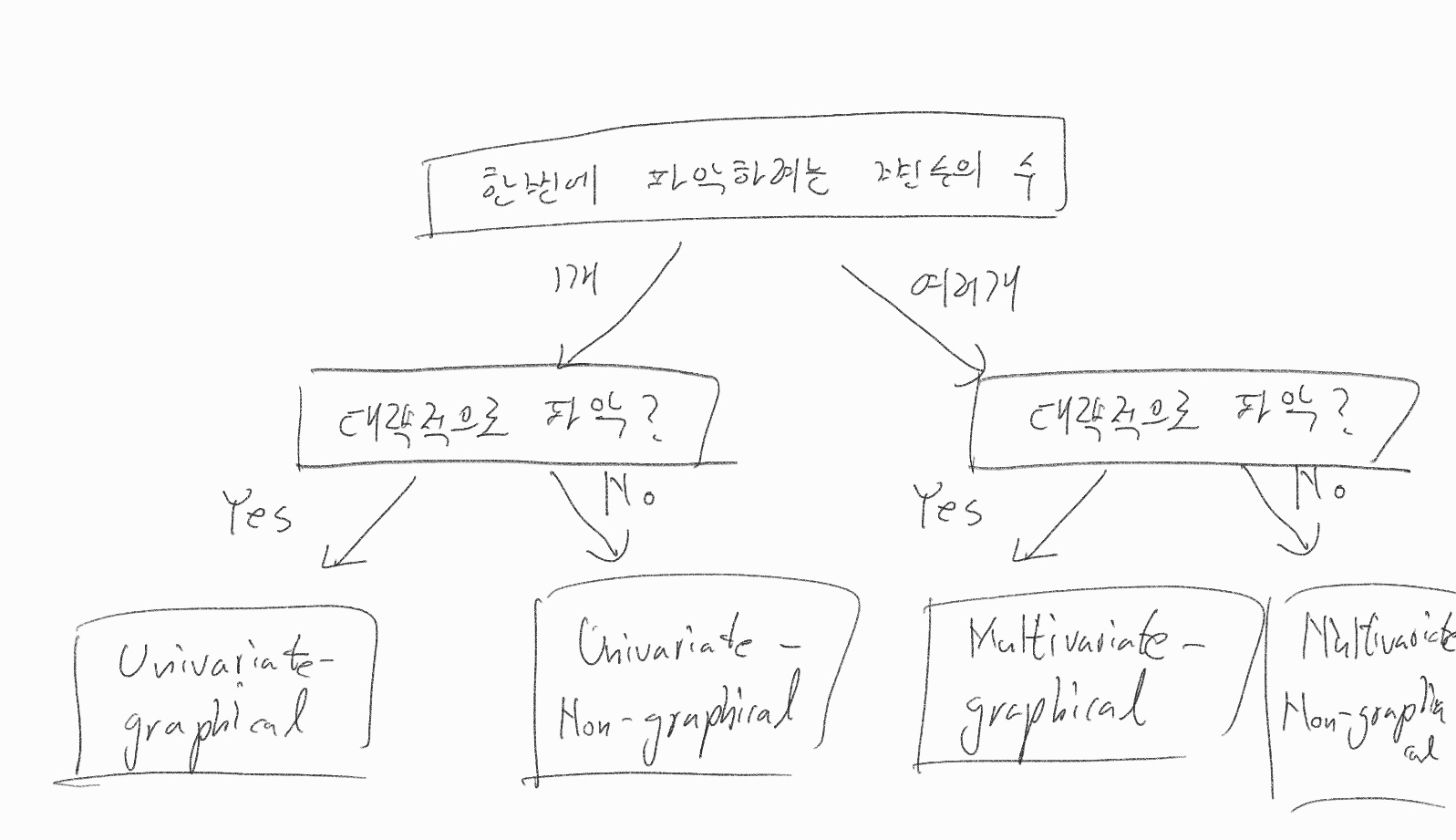
1. 그래프인가?(Graphical)
2. 아닌가?(non-graphical)
3. 한번에 파악하려는 변수가 하나인가?(Univariable)
4. 아니면 여러개인가?(Multivaliable)

• 그래프로 표현하는가?(Graphical or non-graphical)

먼저 데이터를 그래프로 표현하느냐 아니면 숫자로 표현하느냐 입니다.

데이터를 그래프로 표현하게 되면 한눈에 데이터를 파악할 수 있으므로 개략적인 형태를 파악할 수 있습니다.

따라서 대략적인 형태를 파악하기 원한다면 그래프(Graphical)로 표현해야하고, 정확한 값이 필요할 때에는 평균이나 분산같은 숫자(non-graphical)로 표현하면 됩니다.

• 한번에 파악하려는 변수의 갯수는 어떠한가?(Univariable or Multivaliable)

이것은 변수를 하나씩 확인 할 것인지 아니면 여러 변수를 동시에 확인 할 것인지 여부 입니다.

여기서 중요한 것은 여러 변수를 동시에 확인하기전에 무조건 개별 데이터 먼저 파악 해보아야한다는 것입니다.

Univariate non-graphical EDA

그래프를 이용하지 않는 방법은 숫자로 나타낼수있어 누가 보더라도 같은 값을 나타내기에 객관적입니다. 이에 반해 그래프를 이용한 방법은 전체 데이터를 그래프로 나타낼수있어 한눈에 파악할 수 있지만 주관적입니다.

1. 빈도표(Tabulation)

범주형 변수라는 것이 있습니다. 데이터를 범주형 변수로 수집하는 목적은 값의 범위에 포함되는 빈도에 관심이 있어서입니다.

이를 범주형 변수를 표현하는 방법으로 빈도표(Tabulation)가 있습니다.

	남자	여자
count	7	3
proportion	0.7	0.3
percent	70%	30%

이 빈도표를 통해 알 수 있는 것은 입력되지 않은 데이터(missing data)를 파악 가능하다는 것입니다. 즉, missing data가 존재하게 된다면, percent의 합이 100%가 되지 않습니다. 이를 통해 데이터에 missing data가 존재함을 파악할 수 있습니다. 예를 들어, 위에서 남자 70%와 여자 30%의 합은 100%이므로 위 데이터는 missing data가 없다고 생각할 수 있습니다. 또한 이 빈도표를 통해 데이터의 갯수 파악가능(count)하고 구성비 또한 파악가능(proportion)합니다.

2. 표본 통계치(Sample statistics)

양적 변수(Quantitative data)를 EDA 하게 되면 모집단의 분포를 추정할 수 있게 됩니다.

즉, 다음과 같은 center, spread, modality, shape, outliers, skewness, and kurtosis를 파악할 수 있게 됩니다.

각각이 뜻하는 의미는 다음을 참고하시면 됩니다.

Sample statistics

위의 값들은 표본 통계치라고 하는데, 표본 통계치는 모집단 값이라고 추정되는 값이라고 정의 내릴 수 있습니다.

Univariate graphical EDA

1. 히스토그램(Histograms)

히스토그램은 연속형(continous) 데이터를 이용하는 것으로, 파악할 수 있는 것은 central tendency, spread, modality, shape and outliers이 있습니다.

2. 막대 그래프(Bar plot)

막대 그래프는 범주형 데이터를 이용하는 것이지만 연속형 데이터에 사용하면 전체적인 분포를 뺴곡히 파악 가능합니다.

3. 상자그림(Box plot)

상자 수염 그림이라고도 하는데 이것을 이용하면 **outlier, symmetry (데이터 치우침정도)를 파악할 수 있습니다.

4. QQ-plot(Quantile-normal plots)

가지고 있는 데이터의 분포와 가정한 분포를 비교하여 얼마나 일치하는지 확인할 수 있습니다. 이를 이용하여 ** skewness, kurtosis, bimodality**를 파악할 수 있습니다.

x축은 이론상의 데이터(가정한 분포) quantiles, y축은 샘플(가지고 있는 데이터)의 quantiles표시합니다. 여기서 x축과 y축의 분포가 일치한다면 일직선을 그리게 됩니다.

상세한 내용은 아래 링크를 참조하면 됩니다.

Normal Quantile-Quantile Plots

Multivariate non-graphical EDA

한번에 여러개의 변수를 동시에 파악하는 방법 중 그래프를 이용하지 않는 방법입니다.

1. 교차표(Cross-tabulation)

보통은 범주형 데이터에 사용하게 됩니다.

Cross Tabulation: How It Works and Why You Should Use It

2. 상관관계

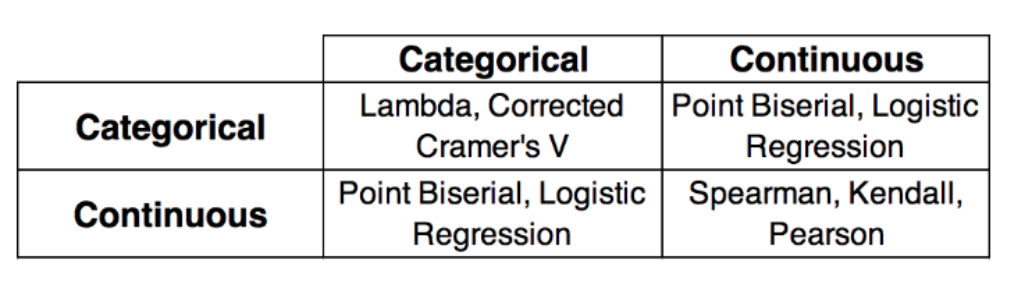
연속형-연속형(Correlation for continous data)

• pearson correlation
• kendall correlation *spearman correlation

범주형-범주형(Correlation for categorical data)

• chi square test
• Cramer’s V

연속형-범주형(Univariate statistics by category)

목적변수가 quantitative이고 설명변수가 categorical 변수일때, categorical 변수의 level에 따라 목적변수를 비교하고자 할때 사용합니다.

• Comparing the means is an informal version of ANOVA.
• Comparing medians is a robust informal version of one-way ANOVA.

• Comparing measures of spread is a good informal test of the assumption of equal variances needed for valid analysis of variance.

• Biserial correlation
• Polyserial correlation

type of correlation

Multivariate graphical EDA

1. Univariate graphs by category

• categorical 변수의 level에 따라 각각 quantitative 변수의 값을 표시
• side-by-side boxplots
• distribution by category levels)

2. 산점도(Scatterplots)

두 개의 변수가 양적(quantitative)일때 사용하는 것으로 outcome variable은 y축에 놓아야합니다. 또한 모양, 색, 크기 등으로 categorical 변수를 산점도에 표시 가능합니다. ————————————————————————————————

덧붙임(Appendix)

강건성(Robustness)

참고로 중앙값(median)은 강건성(robustness) 성질을 가지고 있습니다. robustness란 데이터에 이상치가 포함되었을때 통계값이 변하지 않으려는 경향을 이야기합니다.

표준편차(Standard deviation)

Why we need standard deviation instead of variance

왜도(Skewness)와 첨도(Kurtosis)

Skewness(asymmetry) and kurtosis(peakedness compared to a Gaussian dist.)

Skewness > 0 이면 오른쪽으로 꼬리가 긴 분포입니다.
kurtosis > 0 이면 꼬리가 더 두꺼워지고 , 가운데가 뾰족해집니다.

왜도(Skewness)와 첨도(Kurtosis)

Reference

• CMU Statistics
• https://www.youtube.com/user/jbstatistics